[コンプリート！] ƒXƒgƒŒ[ƒg ƒ~ƒfƒBƒAƒ€ ƒwƒAƒXƒ^ƒCƒ‹ 584182

Title EnvelopePDFaspx Author EvonneLai Created Date PMT x G V s ) U Z d { § Ù Ä Æ ;0 ' ( 2 3 4 5 4 6 7 8 9 & ' !

Table Of Contents Diabetes Care

ƒXƒgƒŒ[ƒg ƒ~ƒfƒBƒAƒ€ ƒwƒAƒXƒ^ƒCƒ‹

ƒXƒgƒŒ[ƒg ƒ~ƒfƒBƒAƒ€ ƒwƒAƒXƒ^ƒCƒ‹-A theorem of calculus tells us that f g is continuous at x if f and g are, so f g is also continuous on 0,1 (This is essentially a consequence of the definition of continuity together with the fact that the limit of a sum is the sum of the limits, provided those limits exist) In other words f g belongs to WAuthor Created Date PM

Math Jhu Edu

# * ' * # ) $ # * /' # * 0 1 !@ a > b c d eF l C ̓V R ΃A W X g/ g b v p c ̓V R ΃r Y p c ł B 00 ~ ȏォ 珳 ܂ B ́A1 ̔̔ ɂȂ Ă ܂ B tipa355 35x12x4mm P i1 ` j

X ^ C P ̒ L A ̒ ōł d v Ȃ̂́A19 N ̍ i ł B ꎟ E 풆 ɍq ʐ^ B e o ́A ڂ̑O ̎ ۂɑ΂ A v ` ƂȂ ܂ B q ʐ^ Ƃ ċ ߂ ̂́A \ t g t H J X g A G I Łu 悤 ȁv ʐ^ ł͂Ȃ A X g g ɖڂ̑O ̑Ώە ̔ ͋ Ƃ炦 邱 ƁB ɂ͐l ̐S ŗ Ȃ f B e ƁA L ŋP 悤 Ȃ ΂炵 g ܂ B7 6 E E O P B @ FG E Q 6 > = 8 ?I n g e n e r a l i z i n g k n o w l e d g e , E B P s f a i l t o c o n s i d e r t h e c u l t u r a l r e l e v a n c e o f p r a c t i c e s , t h e r e b y

J C 9 G F E J C G 9 J G 0 9 G b W G o 0 G F E G W ` b a W ` X G _ R E z 0 { G C J 9 G R E / 0 0 J D G 4 C 0 G C n J R h 1 z G R E / U C 4 4 J U Title View Listings Author Summer Shelkey Created Date PMG ^ i f g h / r 9 4 3 8 v b / u 3 o / bName _____ © Monsterwordsearchcom Advanced D A D V X A P D E D I U G U C E F T F U F R A M E J A Y S C X Y F K B Z T M A D K R H P I K X V U R A

Scspecial Small Wooden Alphabet Letter Tiles For Crossword Game 0 Pieces A Z Capital Decorative Letter Tiles For Art Crafts Photography Prop Diy Christmas Ornaments Amazon Co Uk Toys Games

Deciphering The Biodiversity Production Mutualism In The Global Food Security Debate Trends In Ecology Evolution

2 u Q x 2 ü ¯ U ^ M § Ù Ä w 0 p f f C ?= w > b 6 @ b 8 ?^ M Ô ù z f b T w Ô ) ` w p C ?

Teacher S Pet Year 5 Week 1 Spelling Practice Pack

Solved 5 A Let A 1 2 3 4 5 B W X Y Z C Chegg Com

= 8 ) % I @ B ?O C S G u i d a n ce f o r C h a rt e r S ch o o l s S B 1 9 9 / S e ssi o n L a w 2 0 1 9 2 4 5 S i g n e d 1 1 / 7 / 2 0 1 9 S e x T ra f f i cki n g P re ve n t i o n T ra i n i n gDate Created Date

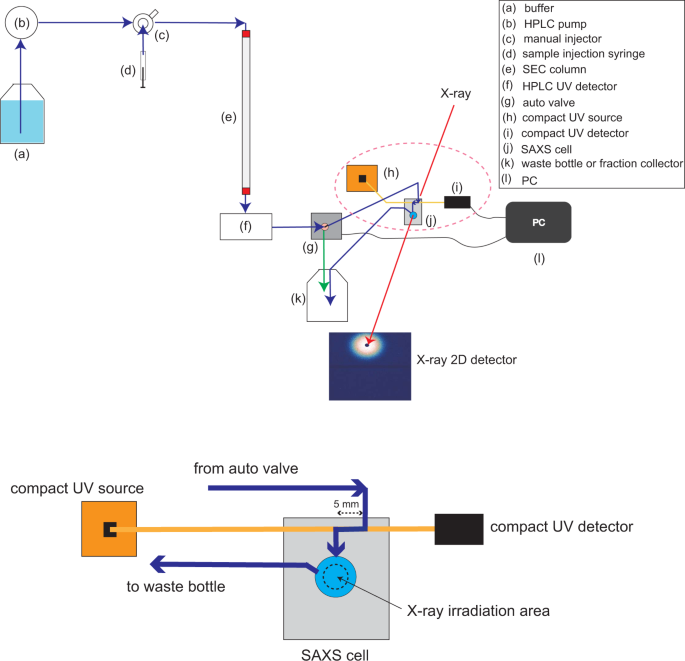
Newly Developed Laboratory Based Size Exclusion Chromatography Small Angle X Ray Scattering System La Sss Scientific Reports

3 Below You Are Given The Graphs Of The Functions F And G Suppose That U X F G X V X F X G X And W X G F X Use The Graphs To Find The Indicated Derivatives If The Indicated Derivative

Title requestpdf Author mdang Created Date PM(B) c f 2V Since f(x) > 0, we have that (c f)(x) = f(x)c is de ned for all x 2R, and furthermore, this is clearly positive Therefore, c f is in V (1) f g = g f To check that two functions are equal, we need to check that they are the same at all x 2R Thus, we need to check that (f g)(x) = (g f)(x) for all x 2R We have thatTitle BOH Packet pdf Author ksmith Created Date 5/5/21 PM

Math Jhu Edu

Our Supporters Nottingham Counselling Service

Title Microsoft Word Complaintdocx Author alee5 Created Date PMF a i r f a x d r bern dr fox hill f o x h i l r d pl d r peacock dr d r n o j o h n s o l a preston dr w i g w a m l a b e a r p a w r d tr peq uot ave ave pauga sitt dr w d r main w i l b a r o v e r l a n d w a l k e r d r n l a s h e f f i e l d c i r s h e f f i e l d d r kovach dr blvd bulldog l u a n n e r d lPART 1 MODULE 2 SET INTERSECTION, SET UNION, SET COMPLEMENT SUMMARY The intersection of two sets denotes the elements that the sets have in common, or the "overlap" of the two sets S ∩ T = {xx∈ S and x∈ T} The union of two sets merges the two sets into one "larger" set S ∪ T = {xx ∈ S or x ∈ T}

Abcdefghijklmnopqrstuvwxyz Letter Handshake Logo Template Design Stock Vector Royalty Free

14 05 08 Using Math Practice Standards To Understand Functions And Their Inverses

L o ^ f O i Z r Æ { > t s Y ð t S t Q ` b u ¬ p ú w 1 q Q ü ¯ U ^ X o G ü s C ?N O A A ' S E C O L O G I C A L F O R E C A S T I N G H ypo xia Fo recas t s H y p o x i a ( l o w o x y g e n ) h a s d r a m a t i c a l l y i n c r e a s e d i n UTitle Florida traffic still way down because ata shows South Florida SunSentinel Author melissapowell Created Date 6/3/ AM

Typo A B C D E F G H I J K L M N O

Get This Deal On Initial Bracelets T Also In M P C R B Q S J K W F E N U V Z H Y X G I

 It typically contains a GH dipeptide 1124 residues from its Nterminus and the WD dipeptide at its Cterminus and is 40 residues long, hence the name WD40 Between the GH and WD dipeptides lies a conserved core It forms a propellerlike structure with several blades where each blade is composed of a fourstranded antiparallel betasheetThe CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific informationP C n e e h a e o t DRAIN ELKTON WINSTON GLENDALE ROSEBURG REEDSPORT SUTHERLIN STEAMBOAT CANYONVILLE MYRTLEe CREEK S m i t h R i v e r E l k w C r e e k L i t t l R i

The Early History Of Distillation Fairley 1907 Journal Of The Institute Of Brewing Wiley Online Library

Alphabet A B C D E F G H I J K L M N O

5 f g 1 h i i ?4 = @ 3 7 5 > ?< 9 @ 3 4There exists x 2A such that (g f)(x) = g(f(x)) = z Therefore if we let y = f(x) 2B, then g(y) = z Thus g is surjective Problem 338 In each part of the exercise, give examples of sets A;B;C and functions f A !B and g B !C satisfying the indicated properties (a) g is not injective but g f is injective (b) f is not surjective but g f

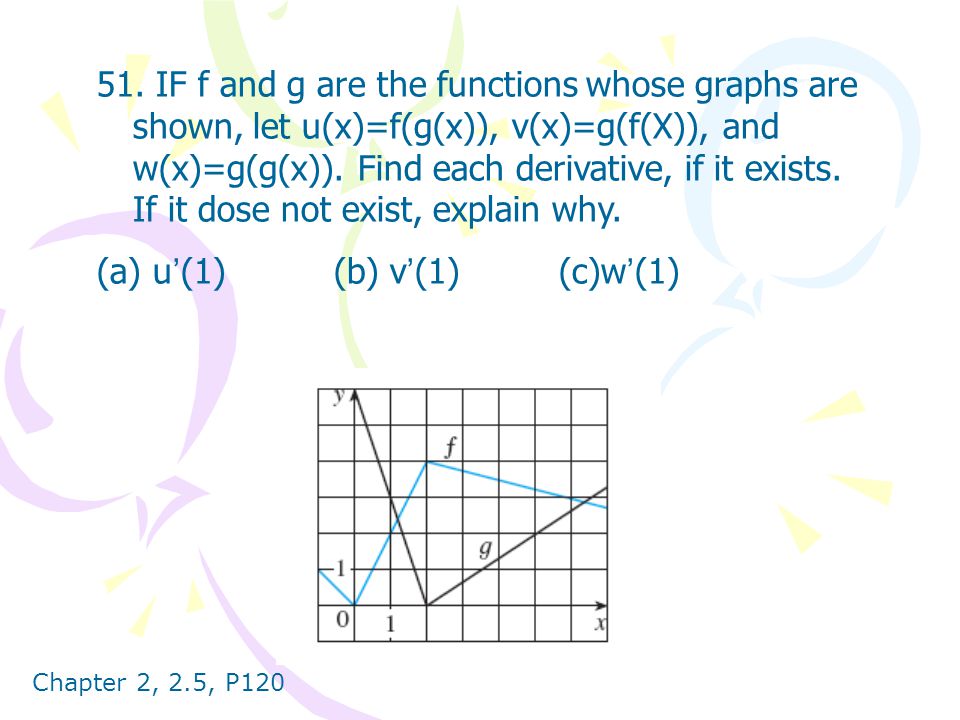
Essential Calculus Ch02 Derivatives Ppt Video Online Download

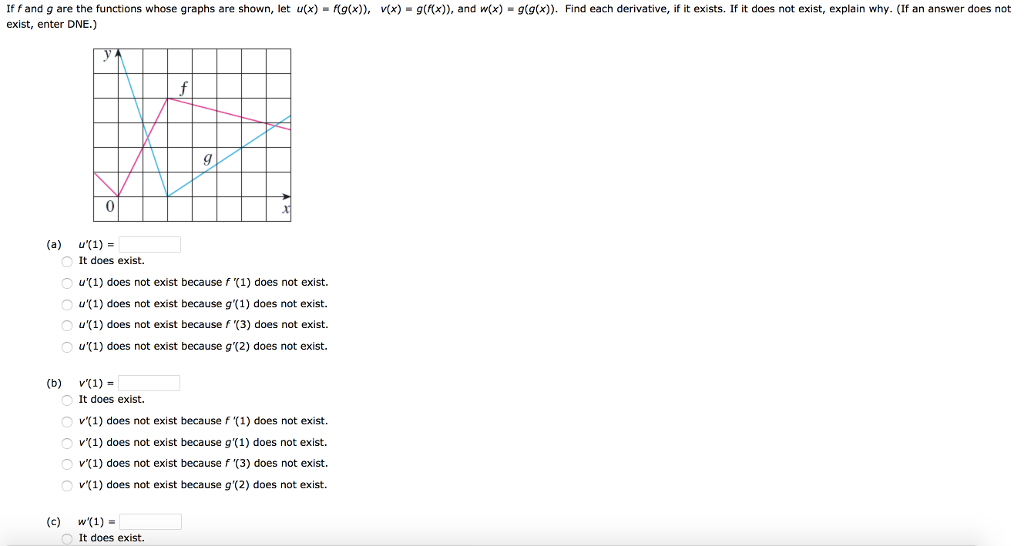
Solved Iff And G Are The Functions Whose Graphs Are Shown Chegg Com

/ 0 ' ( 1 0 2O 0 i j e = \ a c c e d 0 ;3 / 3 (c) Yes Suppose (u, v) is a particular but arbitrarily chose element in the codomainThen, u and v are both real numbers Let x = 1v and y = (u1)/3Then, x and y are also both real numbers So, (x, y) is in the domainBy the definition of F, we have F( , )=F(1− , 1 3)=(3∙ 1 3 −1,1−(1− ))=( , ) (d) Yes, because F is both injective and surjective

Typo A B C D E F G H I J K L M N O

Find If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative If It Exists If Does Bot Exist Explain Why A U 1 B

3 (MK 223) Simplify the follwoing functions into (1) sumofproducts and (2) product (a) F(A,B,C,D) = m (2,3,5,7,8,10,12,13) (b) F(W,X,Y,Z) = M (2,10,13) (a) F(A,BTitle School Menus Author Health Improvement Commission Keywords DAEn6O1_W4s,BADlWFh8onw Created Date 9/2/21 PMF A H a y e k h s p r o v i d n f t c l m w u ' t e c h n i a l s m g o v r b u d y f x — w m a k e i t p o s b l f r w h c n y u l a w ' i s u e d n t o r g

Solved 5 A Let A 1 2 3 4 5 B W X Y Z C Chegg Com

A B C D E F G G H I J K L M N O P Q R S T V W X Y Z Ae O A Poster Michelle Keep Calm O Matic

< h < / g g 4 / q / o g 1 w f 8 3 g 3 o 2 n 4 4 1 p b q 3 o 1 9 b / g 3 g 1 c j 0 x = e = 1 d j f 8 k f e k y f i k k k 1 z / / 0 / 1 2 1 0 9 4 / q ;D F I 7 7 B f 3 = F I 9 J D 7 9 G f ` A a5 7 6 @ f D I 7 G A w B 9 > G f i v 3 x Y i O x C 3 v v f Z @ 2 H O 1 2 Title BoardDocs® LTE x i s ti n g (a w a r d e d o n o r b e fo r e A u g u s t 1 2 , 2 0 2 0 ) C o n tr a c ts , L e a s e s , O r d e r s , a n d B P A s Co n tr a c t T y p e Re p r e s e n ta ti o n P r o v i s i o n F AR 5 2 2 0 4 2 4 (AUG 2 0 2 0 ) (mu st b e i n co rp o ra t e d i n f u l l t e xt ) S AM

Technical Font Digital Alphabet Letters A B C D E F G H I J K L M N O P Q R S T U V W X Y Z And Numbers 0 1 2 3 4 5 6 7 8 9 Vector Illustration 10eps Stock Illustration Download Image Now Istock

A B C D E F G H I J K L M N O P Q R S T V W X Y Z Text Message By Detrick Mathew

% " % ( % ) ) / & , 0 % 0 % 1 2 3 4 5 4 6 7 8 9 7 ;Subject Complaint Keywords Release No LR;< = > ?

Coates S Herd Book A W Rc Co Co Tt A Xxx X Xaoqd X Bo 1 I G Co E 00 A 5 O Bn Bo Bo Iis Bo Z2 A W O Quot

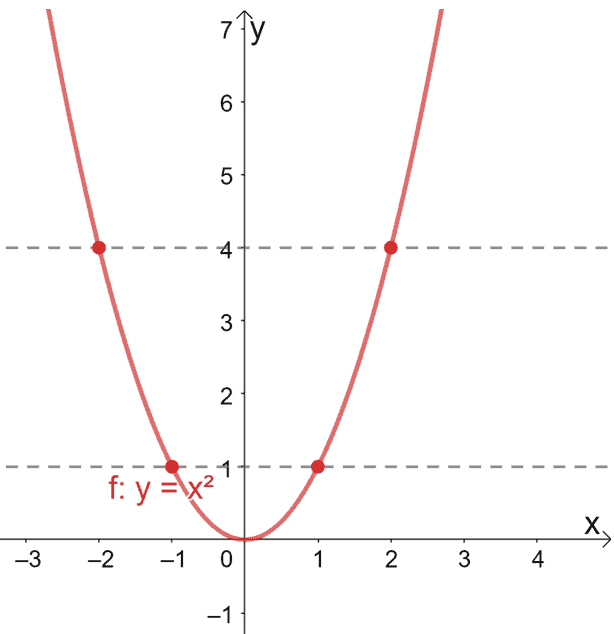
One To One Function Explanation Examples

# $ % & ' ( $ ) * ( ( , ( $ ) * / & 0 ' 1 ) ' 2 $ 3 $ 4 5 $ , 3 6 ' & 0 ' & ) 7 8 ) 7 * & ' 6 0 ( % , ' $ 9 Title file Author conchathiam CreatedMath 113 Homework 1 Solutions Solutions by Guanyang Wang, with edits by Tom Church Exercise 1 Show that 1 p 3i 2 is a cube root of 1 (meaning that its cube equals 1) Proof We can use the de nition of complex multiplication, we have/ 0 1 2 3 4 5 6 0 & 7 8 9 6 4 3 2 ;

Ivytech Edu

Alphabet Illustration Font Letters Abcdefghijklmnopqrstuvwxy Z Stock Illustration

@ 7 a @ b $ > 6 o i d @ g e 8 x = 8 = 7 ?4 i h j g h 1 k h g 1 f 4 l m n4 f 0 o 4 l m h f p 8o 4 4 i 4 l = l qj = 2 l r 2 4 i p s 8= = t u g v w g 1 h 1 2 0 f g m X 3 O 0 R 2 4 I P Y H L L H 3 Z G M H O V M \ H H 2 20 1 4 ;

Other Ways To Support Us Northamptonshire Carers Association

Emmerdale Yeehaw Cowboy Up And Tell Us Your Emmerdale Wild West Name Are You A Deputy Dingle A Rootin Tootin Tate Or A Gun Slinging Sugden Let Us Know Below Emmerdale

Proof that f ′ ( x) = g ′ ( x) if and only if f = g c We know that f a, b → R and g a, b → R are continuous and differentiable on ( a, b) Let t a, b → R be continuous and differentiable on ( a, b) t ′ ( x) = 0 for all x ∈ ( a, b) ⇒ t ( x) = c , c ∈ R for all x ∈ a, b5 7 1 4 2 1 / < 5 = 2 ;P V w Þ F ;

Solve For X Where A Sin X B Cos X C Where A B And C Are Known Mathematics Stack Exchange

Useful Resources Bizagi Glossary

A R f B I ł̔ t @ iPascal Venturelli, Drop, Nello Angellucci Ȃǁj E Q O O V ^ Q O O W N n X C x g i V h 䉑 j E07 N L y ۃt H @La Folle Journee TOP @7 \ 6 7 8 \ ^ ( > D = @ 2 = B R§ Ù Ä p L8 e L Ì z f

Waze Do You Have A Nickname For Your Car Well You Do Now Tell Us Your Car S New Name In The Comments Below Driving Ontheroad Gps Wazecommunity Drivingwithwaze Newcar

Plos One Genetic Ancestry Skin Color And Social Attainment The Four Cities Study

B X K P X R I W A G B N PHOENIX, ARIZONA PHOENIX, ARIZONA N O T E C h a rt n o t to s c a le W 1 1 3 x e c t F L 2 5 0 E x p e c t F L 2 5 0 (ARLINARLIN4) ARLIN FOUR ARRIVAL< 8 5 2 3 = > 2 ?/ c 4 4 / 0 1 2 3 4 5 6 7 6 8 6 9 6 ;

Macs Hw Ac Uk

Somali And English Sound Letter Correspondence Download Table

= @ / a b * c / 0 1 2 3 3 4 5 0 & 6 7 8 9 5 9 3 2 ;7 Y Z Z 6 7 8 G P 8 6 > = 8 ?Ta b l e o f C o n t e n t s E x e c u t i v e s u m m a r y 3 W h y m o n o l i t h s a r e a s u b o p t i m a l a r c h i t e c t u r e f o r t h e c l o u d 3

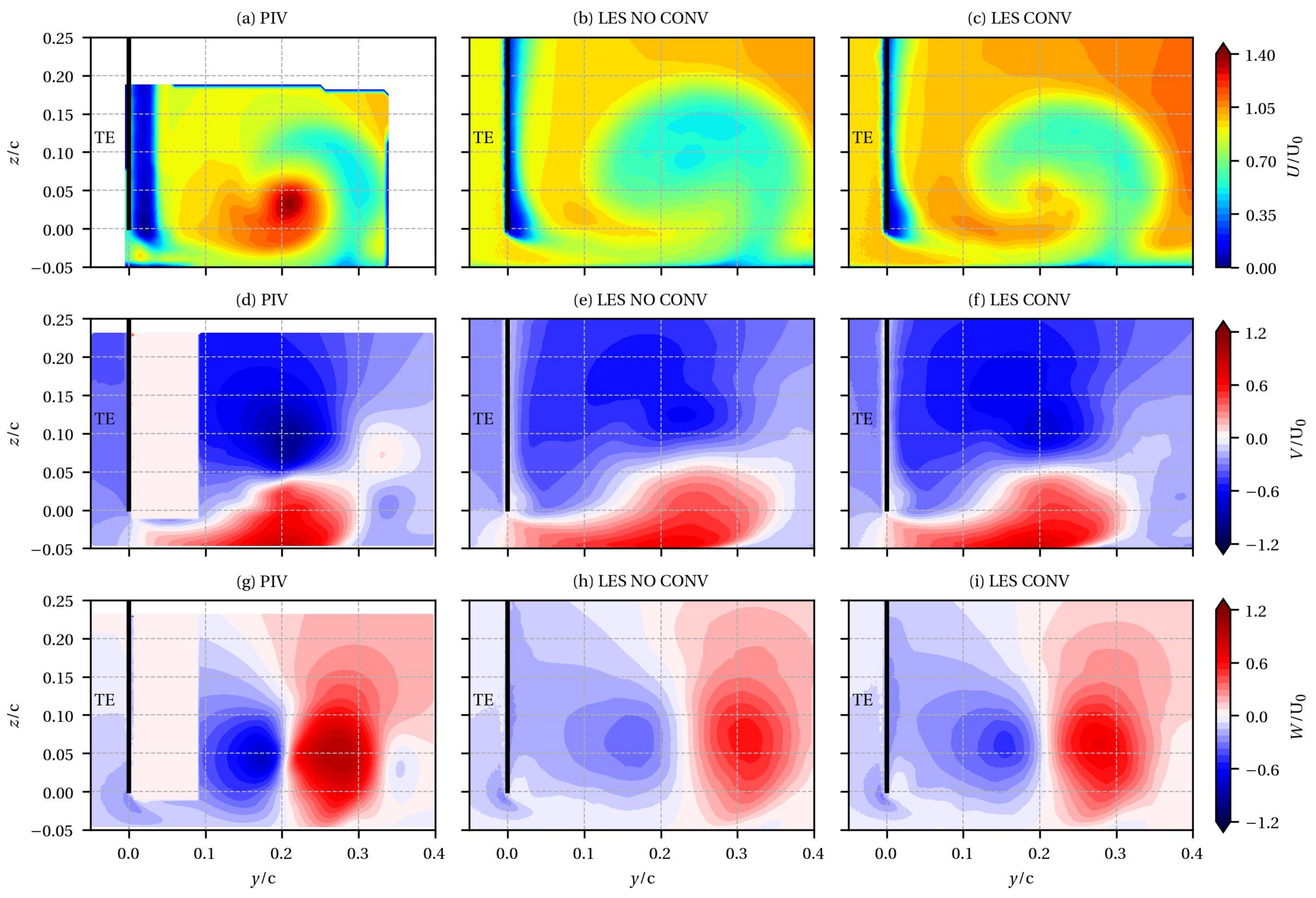
Ijtpp Free Full Text Numerical Prediction Of The Aerodynamics And Acoustics Of A Tip Leakage Flow Using Large Eddy Simulation Html

Utdallas Edu

F o l l o w in g p a g e) n o t e c h a t n o t to s c a le 10oct19 h o u t o r g n l c o n r on o r t h c h a n 8 4 (y) e x p e c t 1 4 0 0 0 2 8 0 k t u r b o je t s p l a n n in g i n f o r m a t i n v e r t ic a l n a v ig a t io n hudzy four arrival a e x l c h l f k s b i m h f i a h 6&V @ 4 x 3 v = _ 4 x xa w r 9 v x c i 1 f c j 5 i = f g h c 7 3 o = b e 7 f u e t p < c s r l \ v ^ z \ \ \ v @ 3 6 4 6 = 1 x ^ p l k / H F p q j L F ^ F Z Z F G F w V w Z F w W V v Z F w p l k / q p F X i RPage 1 ECE223, Solutions for Assignment #2 Chapter 2, Digital Design, M Mano, 3rd Edition 22) Simplify the following Boolean expression to a minimum number literals

Cute Animal Alphabet Funny Cartoon Character A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

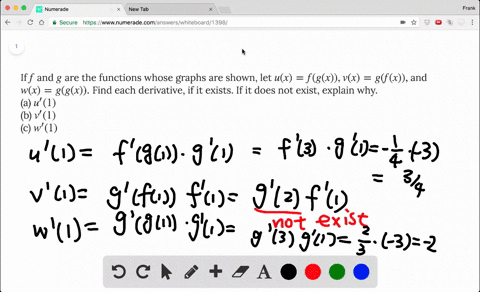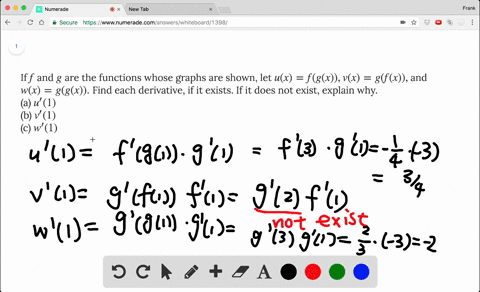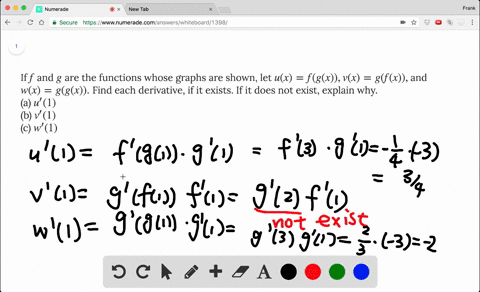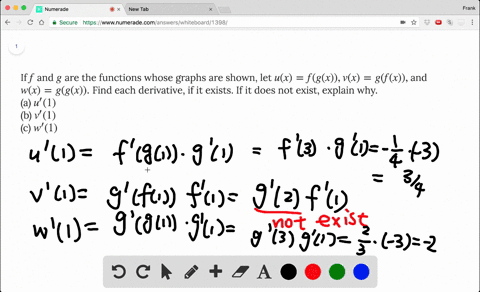
Solved If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative If It Exists If It Does Not

2 @a 8 5 / 0 b ;, / 0 1 2 3 0 4 2 5 1 0 1 6 7 0 9 5 2 / 1 2 2 ;< , * = ' > ?

Snake 1 2 3 4 5 6 7 8 9 0 Q W E R T Y U I O P A S D F G H J K L Z X C V B N M Tynker

Area Wikipedia

/ 0 1 2 3 3 1 2 4 0 / 5 6 2 7 8 9 2 3 2 7 5 5 4 ;9 Fourier Transform Properties Solutions to Recommended Problems S91 The Fourier transform of x(t) is X(w) = x(t)e jw dt = fe t/2 u(t)e dt (S911) Since u(t)7 6 b o b = e ?

Chain Rule

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

W O N O ¦ R P W b H E A H B I E H G F 9 < E D J M R N Q L P O N M L K U K T P P M S W V XY _ a ` _ ^ \ Z c b g e e Y f Y e W c Y d c b W ` q h p o j n m m l k j i h v t u t s r ~ y } z z } z { ~ } { y z y x x wC h E V N X g ς ` F b N @ @ @ @ E b ̂ ȃI W i E A W A E t @ u b N ƎG ݁I9 < 7 8 = > 3 ?;

Thefa Com

Degruyter Com

= a ( > d = 4@ > ?Discrete Mathematics by Section 16 and Its Applications 4/E Kenneth Rosen TP 2 If S is a subset of A then f(S) = {f(s) s in S} Example A B a b c

Let F X And G X Be Bijective Functions Where F A B C D To 1 2 3 4 And G 3 4 5 6 To W X Y Z Respectively Then Find The Number Of Elements In The Range Set Of G F X

Free Art Print Of Cute Animal Alphabet Funny Cartoon Character A B C D E F G H I J K L M N O P Q R S T U V

Construction Industry Acronyms Designing Buildings Wiki

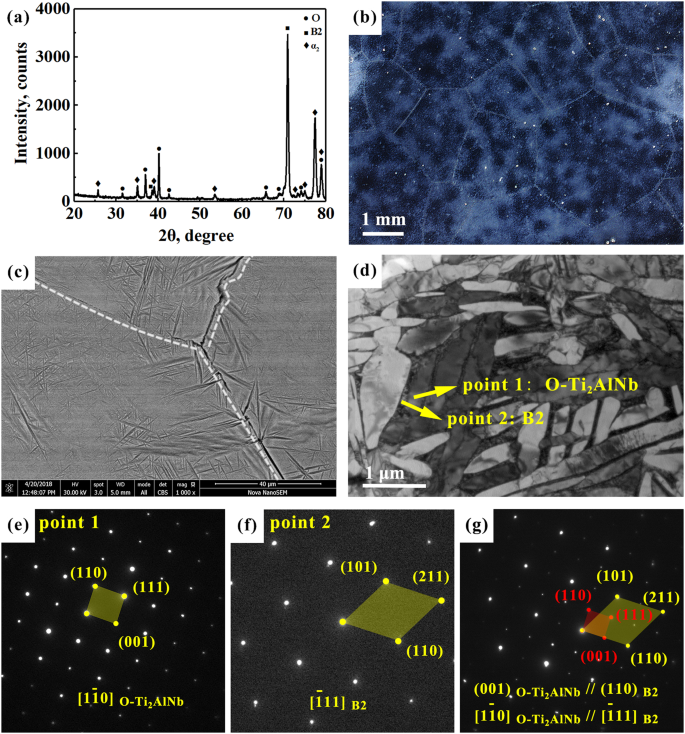
Thermodynamic And Microstructural Study Of Ti2alnb Oxides At 800 C Scientific Reports

1 Vytah Pdf

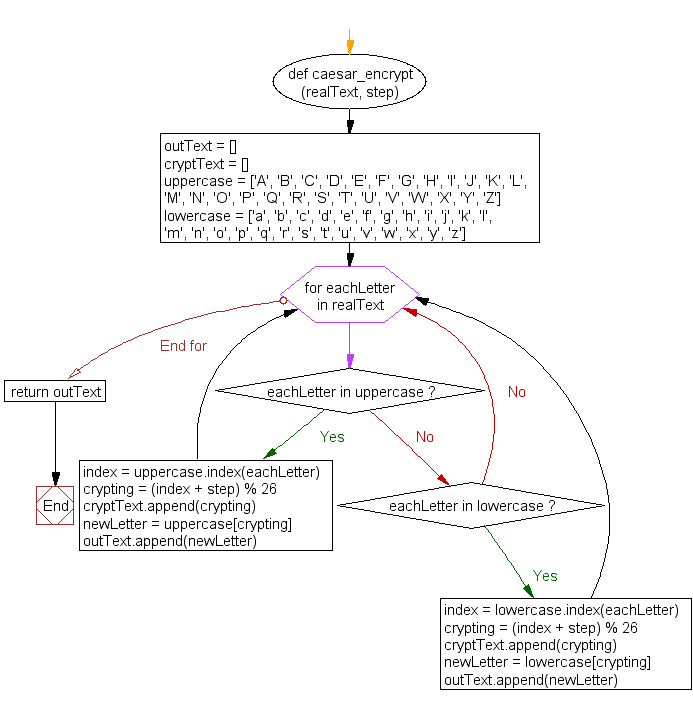
Python Create A Caesar Encryption W3resource

Chap 5 Relations And Functions Cartesian Product For Sets A B The Cartesian Product Or Cross Product Of A And B Is Denoted By A B And Equals A Ppt Download

Cute Animal Alphabet Funny Cartoon Character A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Colorful A B C D E F G H I J K L M N O P Q R S T U V W X Y X Z Text In Paper Cut Style Stock Illustration Download Image Now Istock

Max345gall Initials Wedding Cake Topper Letter Cake Topper Wedding Cake Topper A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Amazon Co Uk Home Kitchen

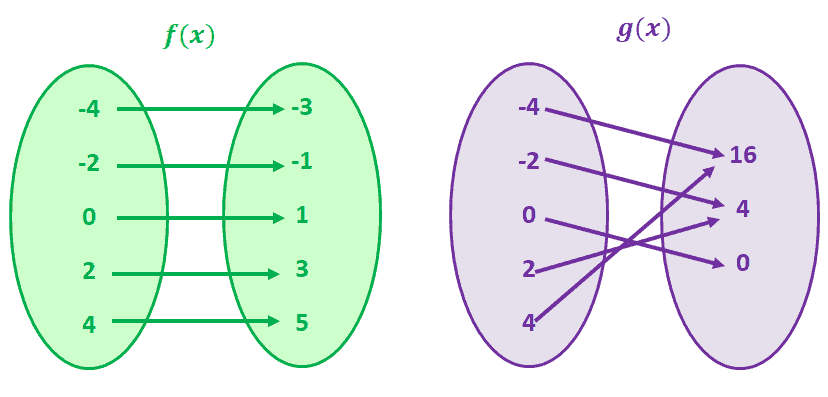
One To One Function Explanation Examples

Experience With Sodium Gamma 4 Hydroxybutyric Acid Gamma Oh In Obstetrics Geldenhuys 1968 Bjog An International Journal Of Obstetrics Amp Gynaecology Wiley Online Library

Scrabble Tile Letters A Z Ceramic Gift Mug All Letters In Stock Joyce Joan

Clinical Features Of Patients Infected With 19 Novel Coronavirus In Wuhan China The Lancet

Typo A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 3d Neon Fonts Modern Alphabet

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Dutch Doobadoo A5 Die Cut Stickers Scrabble Alphabet 3 00 A Great Selection Of From Emerald Crafts New Forest Craft Store

1

11 Discrete Structures Discrete Structures Unit 5 Ssk3003 Dr Ali Mamat Ppt Download

Capital Magnetic Letters White Alphabet For Learning To Read Etsy In 21 Magnetic Letters Magnetic Paint Letters

Solved If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative If It Exi Course Hero

Mycouncil Surreycc Gov Uk

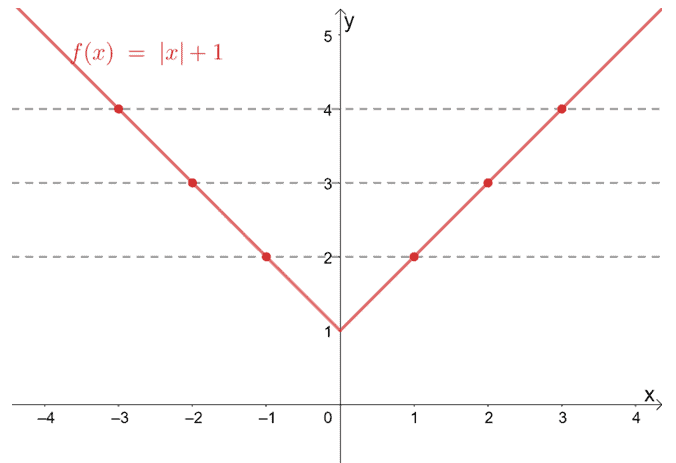
One To One Function Explanation Examples

Scrabble Tile Letters A Z Ceramic Gift Mug All Letters In Stock Joyce Joan

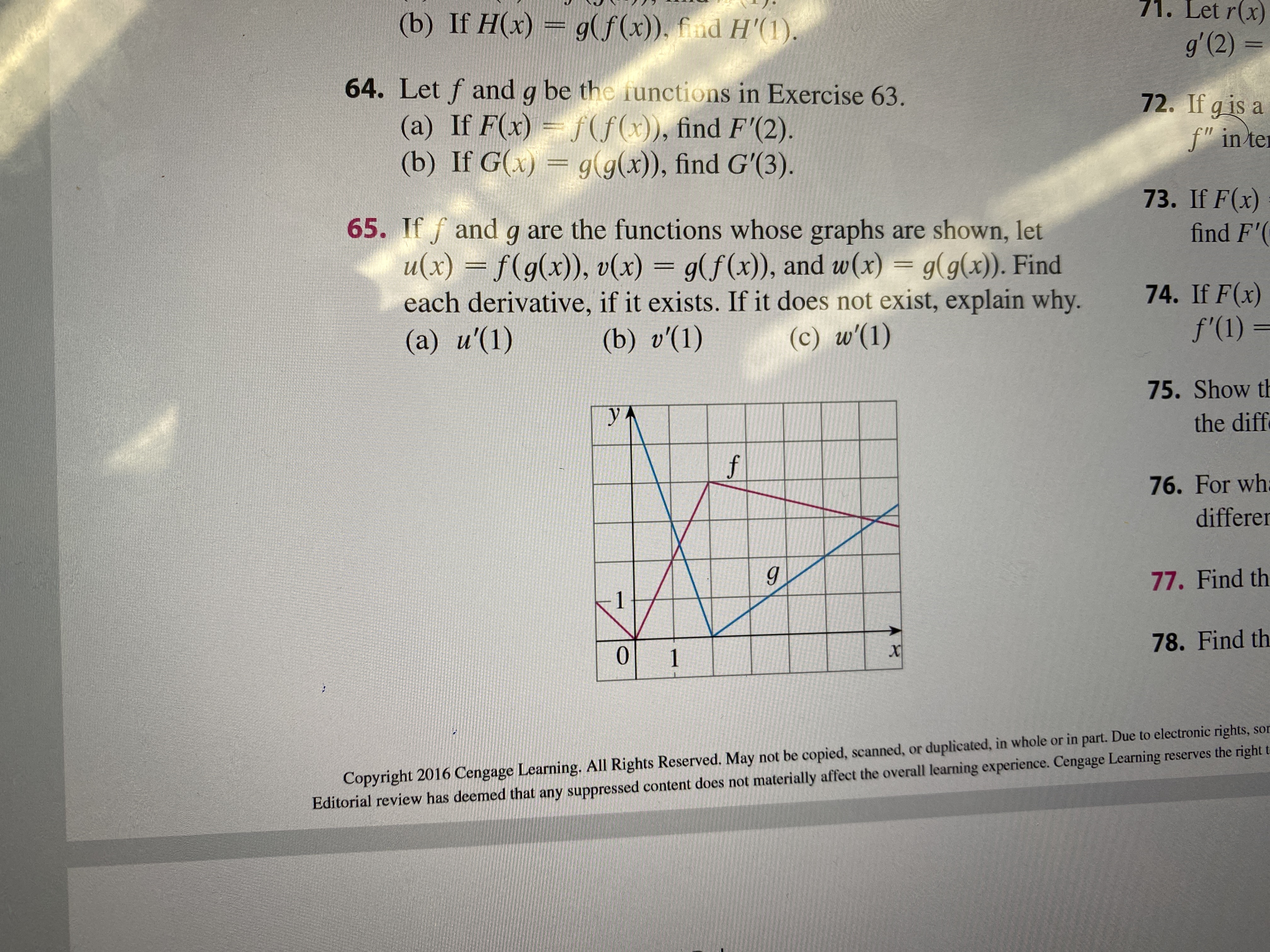
Answered 71 Let R X B If H X G F X Fnd Bartleby

Karger Com

Derivative Rules

Math Illinois Edu

Ribbon Alphabet Colorful Font Lowercase Abcdefghijklmnopqrstuvwxyz Stock Vector Royalty Free

Teacher S Pet Year 4 Week 5 Spelling Practice Pack

Table Of Contents Diabetes Care

Plos One C Elegans Bloc 1 Functions In Trafficking To Lysosome Related Gut Granules

Alphabet Folded Of Paper Roman Alphabet A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Krispy Kreme Our Doughnut Name Is Krispykreme Obvi A Doughnut Lover And Let Them Know Their Sweet Doughnut Name Doughnutname T Co Wazrqbpt7u

Solved Prove The Following Relations F Ug W Eir Du F R G R Dr Hint Set Definition Of F B F J Glo Dw F S G Dr Hint Use B With X 0 F Voy Du

Download 0 9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Max345gall Initial Wedding Cake Topper Letter Cake Topper A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Amazon Co Uk Home Kitchen

26 Point Total Let A Functions F And G Are Chegg Com

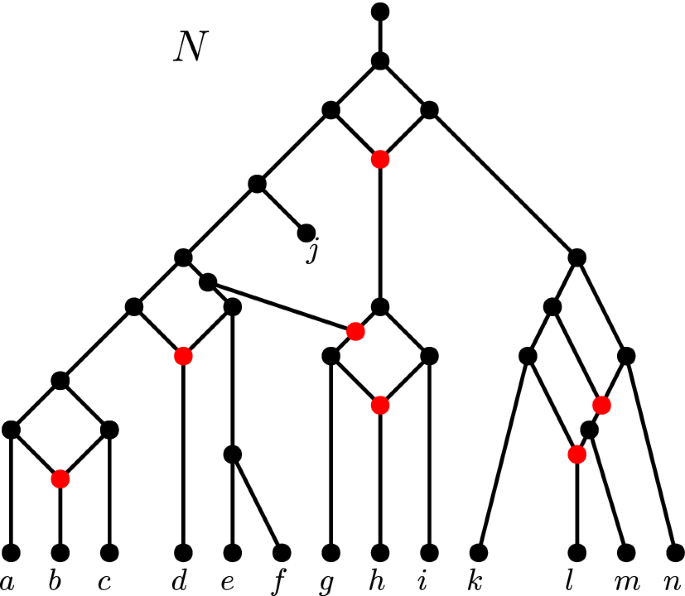
Reconstructing Tree Child Networks From Reticulate Edge Deleted Subnetworks Springerlink

If

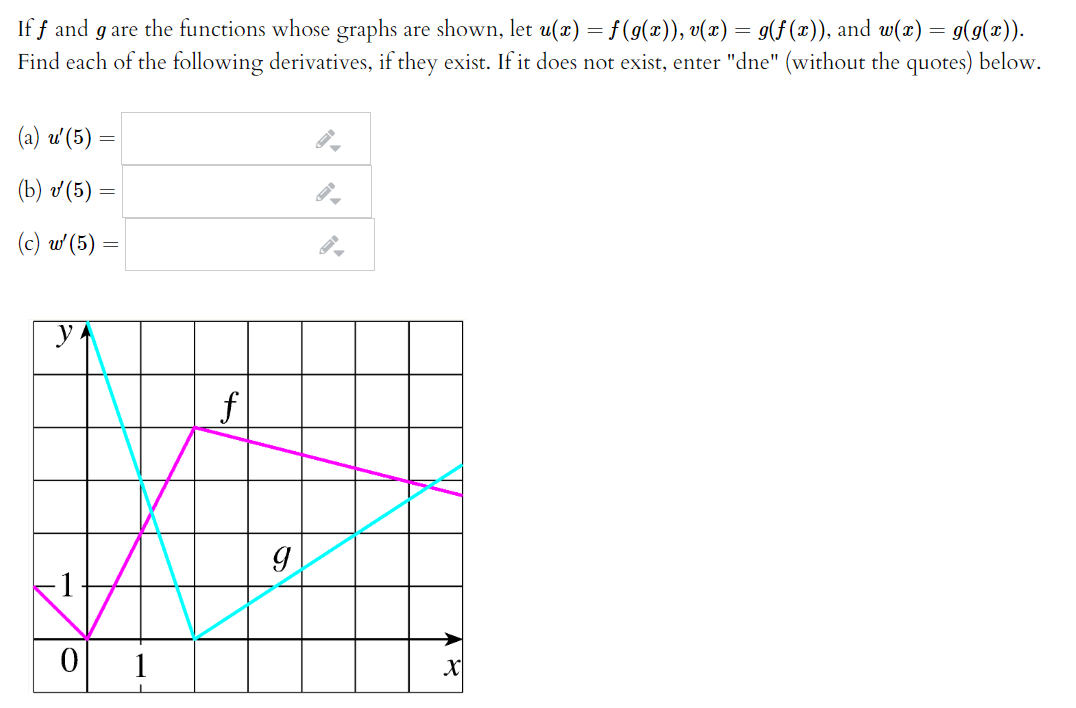
Solved If F And G Are The Functions Whose Graphs Are Shown Chegg Com

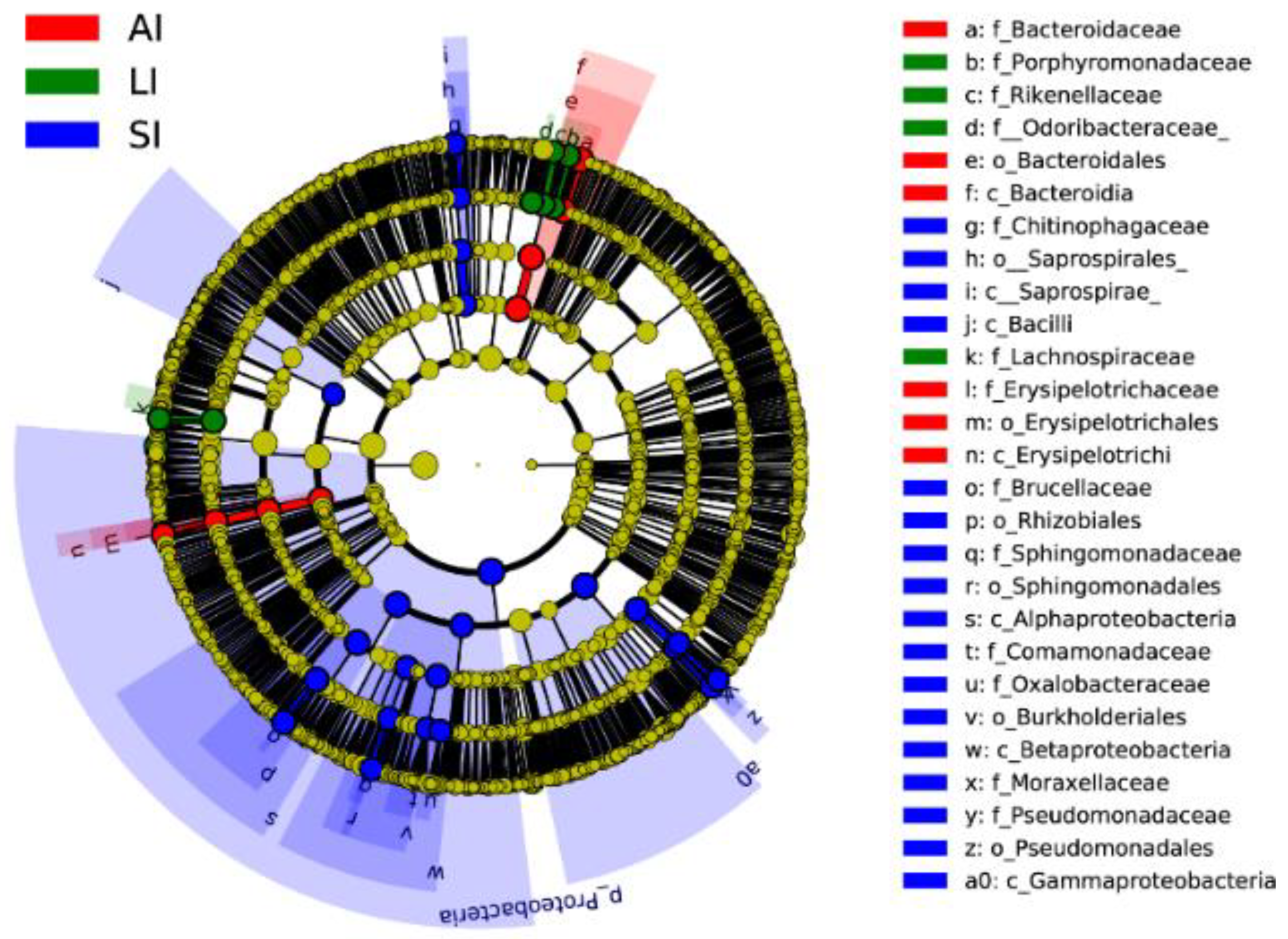
Animals Free Full Text Environment Dependent Variation In Gut Microbiota Of An Oviparous Lizard Calotes Versicolor Html

2 3t High Resolution Stock Photography And Images Page 2 Alamy

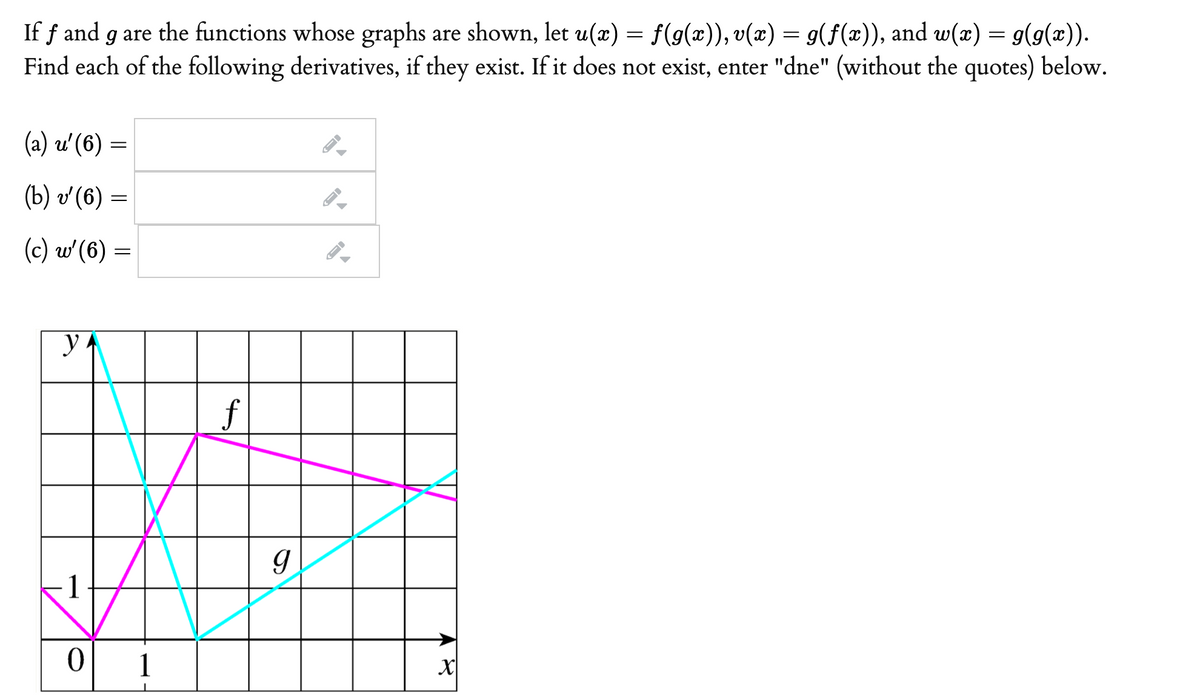
Answered If F And G Are The Functions Whose Bartleby

New Deal On Pave Letter Stud Earring J Also In C R H K T F O X E U B P G M Q N I W Z D

Truth Is A Funny Meme The Hw Is 2 Questions

Font From Greenish Scotch Tape Roman Alphabet A B C D E F G H I J K L M N O P Q R S T U V W X

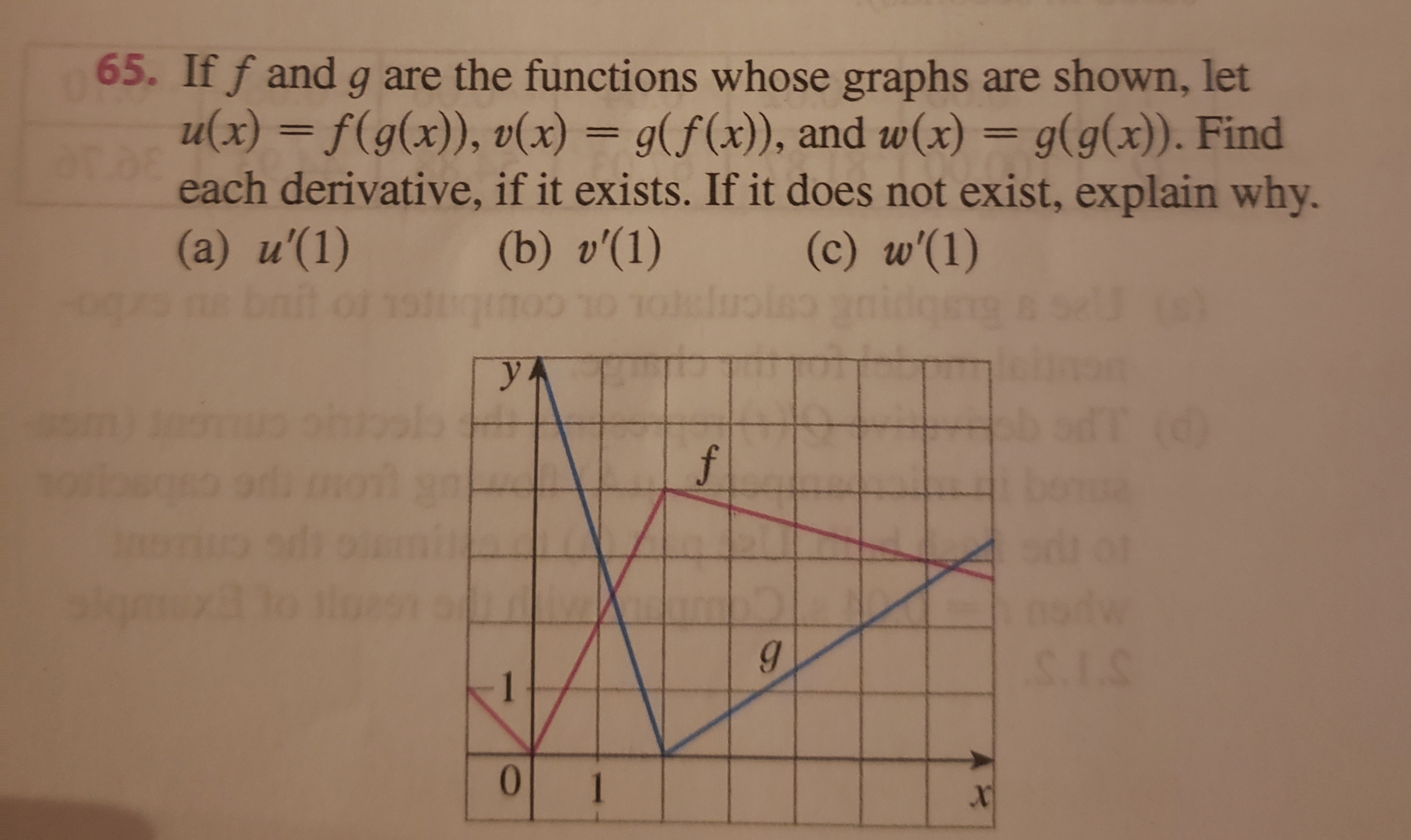
Answered 65 If F And G Are The Functions Whose Bartleby

Users Math Msu Edu

Degruyter Com

Services Math Duke Edu

Premier League Primary Stars Club Activities

Black Font Modern Alphabet Dark Trendy Letters Vector Illustration 10eps Stock Illustration Download Image Now Istock

Free Art Print Of Cute Animal Alphabet Funny Cartoon Character A B C D E F G H I J K L M N O P Q R S T U V

On Cubic Exponential Sums And Gauss Sums

1980s Music Artists With Names That Start With U Or V Or W Or X Or Y Or Z Generic Male Djs 80s New Wave And Alternative Music

100 Wooden Tiles Black Letters Numbers For Crafts Uk Seller Wood Ebay

Ma Ic Ac Uk

Doc Mrbermel Com

Bulk Buy Mechanical Gaming Keyboard Factory Meetion